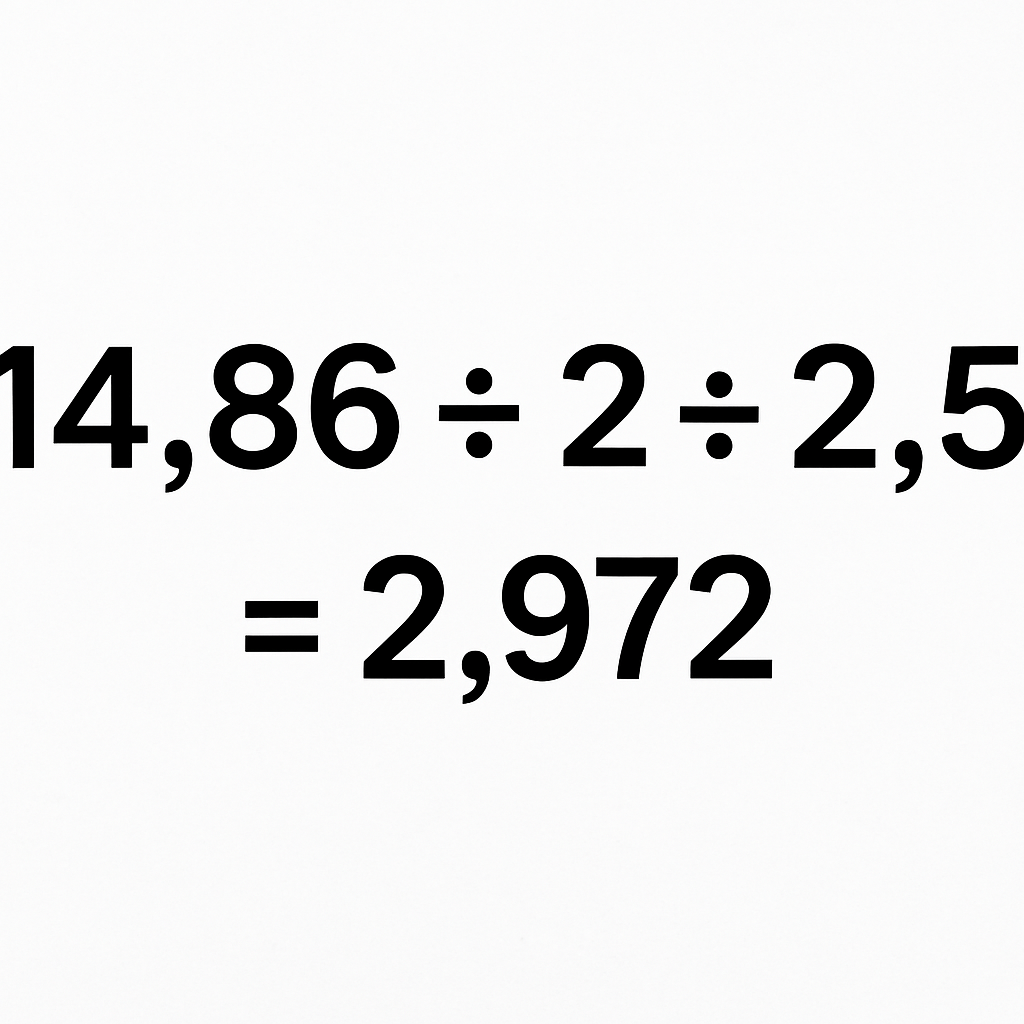Mathematics, in its purest form, is the language of the universe. It helps us define dimensions, understand patterns, calculate costs, and even decode the secrets of nature. Among the myriad of operations and expressions, there are some that appear incredibly simple but can open up a world of insights when explored deeply. One such expression is 14.86/2/2.5.
At first glance, this might look like just another numerical division. A quick calculator check gives you a result of 2.972. But what if we told you there’s more to this number than meets the eye? In this article, we’re going to take an unusual yet fascinating journey into the world of mathematics by exploring the number 14.86, its breakdown through division by 2 and 2.5, and the practical significance of such a calculation in real-world contexts like business, engineering, and finance.
Breaking Down the Expression: 14.86/2/2.5
Let’s begin by understanding the mechanics of the expression.
When you encounter an expression like 14.86/2/2.5, it’s essential to follow the left-to-right rule in arithmetic operations unless parentheses tell you otherwise. Here’s the process:
-
Step 1: Divide 14.86 by 2 = 7.43
-
Step 2: Divide 7.43 by 2.5 = 2.972
The final result is 2.972.
Now, while that’s simple to compute, understanding why this is done and where this matters is where things start to get interesting.
The Number 14.86: Where Might It Come From?
Let’s hypothesize that 14.86 is not a random number but rather a value from a dataset, a measurement, or a cost.
It could represent:
-
14.86 units of currency — say, dollars, euros, or rupees
-
14.86 kilometers/miles — in transportation or logistics
-
14.86 liters — in industrial chemical calculations
-
14.86 hours — in time management or project planning
The divisions by 2 and 2.5 could then represent:
-
Splitting cost/time/distance into halves and further dividing into segments
-
Averaging
-
Resource allocation
Let’s look at this in more real-world scenarios.
Use Case 1: Finance and Budgeting
Imagine you’re managing a budget for a small project, and you’ve allocated $14.86 to a task. You want to split this equally between two sub-tasks (division by 2), and then further divide one of those into 2.5 smaller portions — perhaps different departments sharing resources unequally.
You’d compute:
-
First: $14.86 ÷ 2 = $7.43
-
Then: $7.43 ÷ 2.5 = $2.972
So each of the 2.5 smaller portions would be allocated $2.972. This exactness is crucial in financial planning, ensuring that not even a cent is lost or unaccounted for.
Use Case 2: Engineering and Manufacturing
In engineering, especially manufacturing or material design, measurements like 14.86 cm could represent the length of a material or object that needs to be cut or shaped into segments.
Suppose you’re designing a component where the original length of material is 14.86 cm. You want to split it into 2 parts, and then one of those parts into 2.5 sub-parts for modular assembly. You’d follow the same logic:
-
Each main part: 14.86 ÷ 2 = 7.43 cm
-
Each sub-part: 7.43 ÷ 2.5 = 2.972 cm
Now you have accurately sized segments for a precision component. In mechanical design, that 2.972 cm could be the length of a gear tooth or the height of a structural bracket.
Use Case 3: Data Science and Statistics
Data analysis often involves normalization and partitioning of values. Suppose 14.86 is a data point — maybe an average value or a peak. If you’re processing this through layers (e.g., dividing by 2 for normalization, and 2.5 for feature scaling), then the outcome 2.972 becomes a standardized unit.
In ML models, precision matters. That 0.001 difference could affect predictions, recommendations, or even automated decisions in sensitive applications like healthcare or finance.
The Mathematics of Scaling
Let’s explore a general concept from this: scaling. When you divide a number successively, you’re essentially shrinking it down to more manageable or understandable units.
The formula:
14.862×2.5=14.865\frac{14.86}{2 \times 2.5} = \frac{14.86}{5}
Shows that multiple divisions can be rewritten as a single division by the product of the divisors.
Thus:
14.86÷5=2.97214.86 ÷ 5 = 2.972
This ability to compress or simplify mathematical operations is at the heart of algebra and calculus. It reduces complexity and improves efficiency.
Application in Education
Teachers can use such expressions to explain:
-
The order of operations (PEMDAS/BODMAS)
-
Concepts of simplification
-
Practical utility of mathematics beyond textbooks
A student who calculates 14.86/2/2.5 may initially see it as mere division. But when linked to budgeting, engineering, or even data science, the significance becomes richer.
Why Not Multiply First?
You might wonder, why not rearrange the expression as:
14.86(2×2.5)=14.865\frac{14.86}{(2 \times 2.5)} = \frac{14.86}{5}
You absolutely can — and that’s actually a great shortcut. However, this assumes you understand the associative property of division when working with constants. In applied fields, understanding why you’re dividing step-by-step could reflect resource allocation in stages — e.g., half now, partial later.
So while multiplication of divisors works, it often removes the nuance in real-world situations where each division has its own contextual meaning.
Decimal Precision: Why 2.972 Matters
Let’s pause and appreciate the decimal: 2.972.
Why not round it to 2.97 or 3? Because in critical systems like:
-
Banking — fractions of cents add up to millions over time
-
Aerospace — tiny measurement errors can be catastrophic
-
Medicine — drug dosages must be exact
Decimal precision is non-negotiable. Even in creative industries like digital design or architecture, exact values affect alignment, color, or layout.
Psychological Perspective: The Beauty of Balance
There’s also a philosophical and psychological angle. Splitting something twice — first by 2, then by 2.5 — represents reduction, refinement, and focus.
It mirrors real life:
-
Start with something whole (14.86)
-
Reduce it into manageable halves
-
Further segment it into finer parts
-
Arrive at a core value (2.972)
This process parallels decision-making, design thinking, and even minimalism — distilling complexity into essential values.
Tech Industry: Microtransactions & APIs
If you’re in the digital economy, microtransactions are often fractions of a dollar. Let’s say a subscription cost or service API charge is $14.86 for an entire suite. Dividing this by 2, then 2.5, might give you a per-feature or per-call cost. This micro-calculation can help:
-
Set fair pricing
-
Track usage accurately
-
Prevent overcharging
APIs that deal with cloud functions, storage, or AI queries often bill per thousand or million calls — fractions matter!
Wrapping It All Up: Small Numbers, Big Impact
At the end of the day, 14.86/2/2.5 isn’t just a number — it’s a lesson. It teaches us the importance of simplicity, the relevance of precision, and the surprising depth in something we often take for granted: division.
Whether you’re a student trying to pass a math test, a developer billing API usage, a designer slicing a blueprint, or an entrepreneur budgeting, the number 2.972 may seem small — but it’s backed by a process that reflects accuracy, logical thinking, and real-world applicability.
Sometimes, the most meaningful insights lie in the simplest calculations.
Final Thoughts from Digi Fanzine
Here at Digi Fanzine, we believe in exploring the everyday magic of numbers, ideas, and innovations. By diving deep into concepts like 14.86/2/2.5, we aim to bridge the gap between theory and practice, showing how even the smallest values carry weight in our digital and physical worlds.
Stay curious. Stay calculated. Stay tuned.